兩參數威布爾分佈與刀具損耗

兩參數威布爾分布（Weibull Distribution） 可能是以使用時數建模失效時最常用且擬合效果最好的模型。

研究表明，針對機械可靠度和刀具磨損等場景，威布爾分布在決策支援和故障預測上顯著優於指數分布。例如，一項基於機器可靠度分析的對比研究發現，威布爾模型在反映系統從隨機失效期到磨損失效期的全生命週期性能方面，表現出更高的判別力與決策價值。

威布爾分布

威布爾分布是一種常用於可靠度工程與生存分析的連續機率分布，其 PDF（概率密度函數）與 CDF（累積分佈函數）分別定義為：

PDF

f(t\mid \gamma, \beta) = \frac{\gamma}{\beta^{\gamma}}\,t^{\gamma-1} \,e^{-\bigl(\tfrac{t}{\beta}\bigr)^{\gamma}}\,, \quad t\ge0,\;\gamma>0,\;\beta>0,

CDF：為 PDF 的積分

F(t\mid \gamma, \beta) =1 - e^{-\bigl(\tfrac{t}{\beta}\bigr)^{\gamma}}\,.

期望值（平均壽命）：為 PDF 的期望值計算結果

E[T] =\beta\,\Gamma\Bigl(1 + \frac{1}{\gamma}\Bigr)\,.

形狀參數 $\gamma$

$\gamma<1$
耗損率隨時間遞減，代表刀具在初期磨合階段較易出現早期破損。
$\gamma=1$
耗損率恆定，退化成指數分布，代表刀具在使用過程中磨損與自我恢復達成動態平衡。
$\gamma>1$
耗損率隨時間增加，代表刀具進入磨損期或老化期，磨耗加劇。

給定 $\beta=1$ 時， $\gamma$ 對刀具耗損的影響如下：

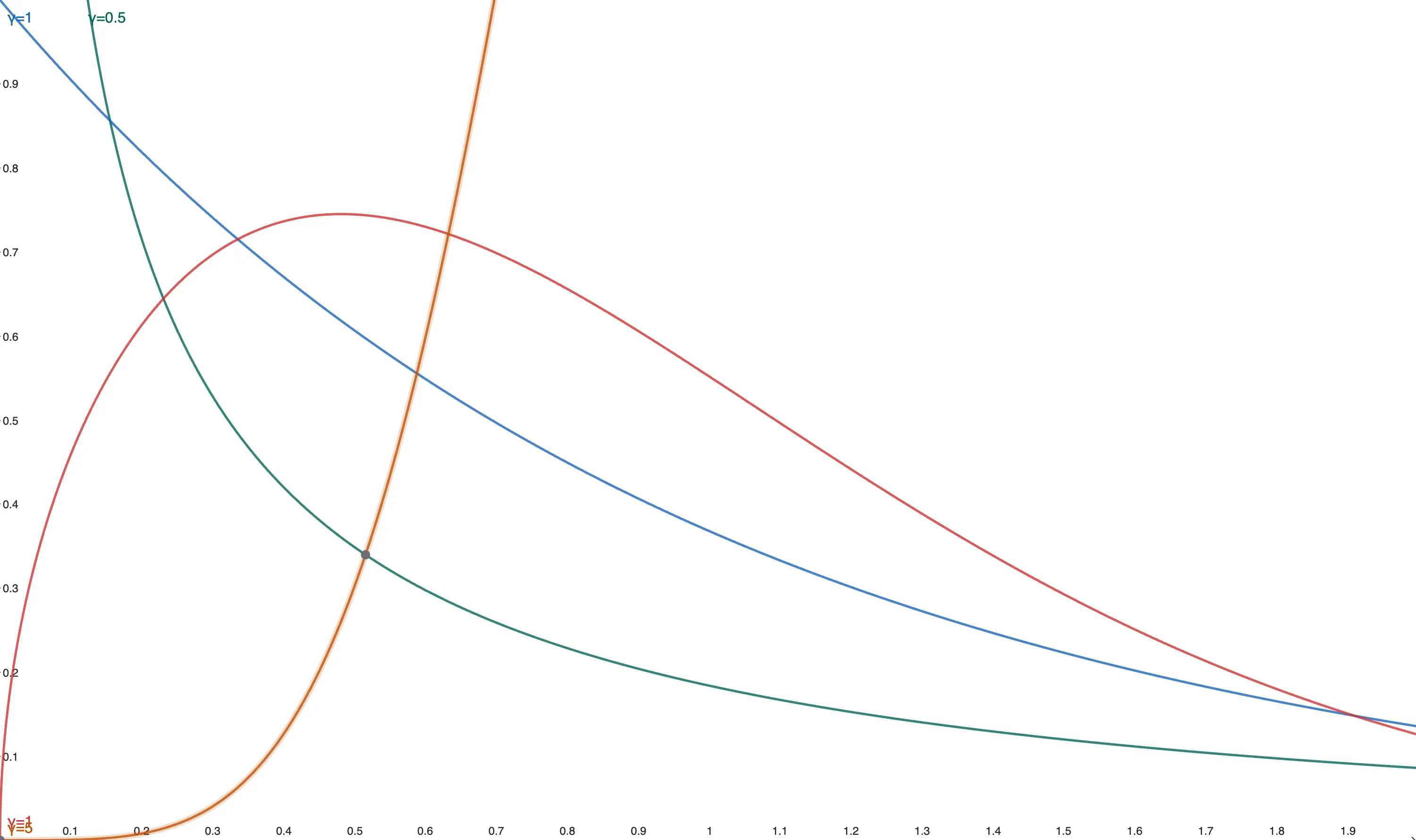
fix-beta

綠色： $\beta = 1, \gamma = 0.5$ ，故障率隨時間遞減，表示「嬰兒期故障」
藍色： $\beta = 1, \gamma = 1$ ，退化為指數分布，故障率恆定
紅色： $\beta = 1, \gamma = 1.5$ ，故障率隨時間增加，表示「磨損型故障」
橘色： $\beta = 1, \gamma = 5$ ，「磨損型故障」，增加得更劇烈

尺度參數 $\beta$

$\beta$ 指定分布之水平伸縮，數值越大，代表刀具在相同形狀參數下，其典型失效時間越晚，平均壽命更長。
在製程條件、材質或表面處理改變時，可透過調整 $\beta$ 反映整體刀具性能之提升或下降。

故障率與累積危險函數

有了威布爾分佈，我們可以有以下實用的函數：

存活函數（Survival Function）：從 CDF 計算得來， $S(t) = P(T > t) = 1 - F(t)$

S(t)=1 - F(t) =e^{-\bigl(\tfrac{t}{\beta}\bigr)^{\gamma}}\,.

瞬時故障率（Hazard Rate）： $h(t) = \frac{f(t)}{S(t)}$

h(t) =\frac{f(t)}{S(t)} =\frac{\gamma}{\beta^\gamma}\,t^{\gamma-1}\,.

累積危險函數：累積危險函數為瞬時故障率對時間的積分

H(t) =\int_{0}^{t}h(u)\,\mathrm{d}u =\Bigl(\frac{t}{\beta}\Bigr)^{\gamma} =-\ln S(t)\,.

其中， $h(t)$ 即為刀具於經過時間 $t$ 而尚未失效時，單位時間內瞬時耗損速率。

應用示例

假設某次車削實驗中，依據刀具耗損資料進行回歸擬合，得參數估計為 $\gamma=1.8$ 、 $\beta=120$ （單位：小時）。此時：

瞬時故障率

h(t) =\frac{1.8}{120^{1.8}}\,t^{0.8}\,,

累積危險函數

H(t) =\Bigl(\tfrac{t}{120}\Bigr)^{1.8}\,.

test-data

程式實作範例

透過樣本評估失效率、可靠度與預估最大壽命

C#

using System;
using MathNet.Numerics.Distributions;
// 引入 Weibull 類別，參考 https://numerics.mathdotnet.com/api/MathNet.Numerics.Distributions/Weibull.htm

class Program
{
    static void Main()
    {
        // 報廢時累積使用時間樣本 (小時)
        double[] scrapTimes = { 70, 85, 90, 95, 80, 88 };

        // 使用 Estimate 估計形狀與尺度
        var dist = Weibull.Estimate(scrapTimes, new Random());
        double shape = dist.Shape;
        double scale = dist.Scale;

        // 定義瞬時失效率 h(t) 與可靠度函數 R(t)
        Func<double, double> hazard = t =>
            (shape / scale) * Math.Pow(t / scale, shape - 1);

        Func<double, double> reliability = t =>
            Math.Exp(-Math.Pow(t / scale, shape));

        // 設定當前評估時間點 (小時)
        double tNow = 50;

        // 輸出瞬時失效率與可靠度
        Console.WriteLine($"[t = {tNow:F0}h] 瞬時失效率：{hazard(tNow):F6}");
        Console.WriteLine($"[t = {tNow:F0}h] 可靠度：{reliability(tNow):F6}");

        // 計算在失效率 p 下之壽命 t_p（此處 p = 0.01 → 99% 可靠度）
        double p = 0.01;
        double tP = scale * Math.Pow(-Math.Log(1 - p), 1.0 / shape);
        Console.WriteLine($"預估最大壽命 t_p：{tP:F2} h");

        Console.WriteLine("可將參數儲存至刀具資料檔，以供後續分析使用：");
        Console.WriteLine($"shape: {shape}");
        Console.WriteLine($"scale: {scale}");
    }
}

TypeScript

/**
 * 找不到可用函式庫，使用牛頓法擬合威布爾分佈，計算形狀參數 γ（gamma）與規模參數 β（beta）
 * @param data 報廢時累積使用時間樣本（小時）
 * @returns 物件包含 γ（gamma）與 β（beta）
 */
function fitWeibull(data: number[]): { gamma: number; beta: number } {
    // (1) 初始猜測形狀參數 γ（gamma） = 1.0
    let gamma = 1.0;
    // 收斂容許誤差 tol
    const tol = 1e-6;

    for (let iter = 0; iter < 100; iter++) {
        const n = data.length;
        // Σ ln t_i，對應到對數概似函數中 (γ - 1) ln t_i 的項
        const sumLog = data.reduce((sum, t) => sum + Math.log(t), 0);
        // Σ t_i^γ，對應到概似函數尾部 exp[-(t_i/β)^γ] 的 t^γ 項
        const sum_tg = data.reduce((sum, t) => sum + Math.pow(t, gamma), 0);
        // Σ t_i^γ ln t_i，對應到對 log-likelihood 對 γ 求導時的中間項
        const sum_tg_ln = data.reduce((sum, t) => sum + Math.pow(t, gamma) * Math.log(t), 0);
        // Σ t_i^γ (ln t_i)^2，用於計算 f'(γ)
        const sum_tg_ln2 = data.reduce((sum, t) => sum + Math.pow(t, gamma) * Math.pow(Math.log(t), 2), 0);

        // (2) 計算目標函數 f(γ)
        // f(γ) = (Σ t_i^γ ln t_i)/(Σ t_i^γ) - (1/n) Σ ln t_i - 1/γ
        // 代表對數概似函數對 γ 的一階導數（score function）
        const f = sum_tg_ln / sum_tg - sumLog / n - 1 / gamma;

        // (3) 計算 f'(γ)
        // f'(γ) = [Σ t_i^γ (ln t_i)^2 * Σ t_i^γ - (Σ t_i^γ ln t_i)^2] / (Σ t_i^γ)^2 + 1/γ^2
        const fprime =
            (sum_tg_ln2 * sum_tg - sum_tg_ln * sum_tg_ln) / (sum_tg * sum_tg) +
            1 / (gamma * gamma);

        // (4) Newton–Raphson 更新：γ_new = γ - f(γ)/f'(γ)
        const newGamma = gamma - f / fprime;
        if (Math.abs(newGamma - gamma) < tol) {
            gamma = newGamma;
            break;
        }
        gamma = newGamma;
    }

    // (5) 計算規模參數 β 的閉式解：
    // β = [ (1/n) Σ t_i^γ ]^(1/γ)
    const beta = Math.pow(
        data.reduce((sum, t) => sum + Math.pow(t, gamma), 0) / data.length,
        1 / gamma
    );

    return { gamma, beta };
}

// 報廢時累積使用時間樣本 (小時)
const scrapTimes: number[] = [70, 85, 90, 95, 80, 88];

// 擬合威布爾分佈，得到形狀參數 γ (shape) 與尺度參數 β (scale)
const { gamma: shape, beta: scale } = fitWeibull(scrapTimes);

// 定義瞬時失效率 h(t) 與可靠度函數 R(t)
const hazard = (t: number): number => (shape / scale) * Math.pow(t / scale, shape - 1);
const reliability = (t: number): number => Math.exp(-Math.pow(t / scale, shape));

// 設定當前評估時間點 (小時)
const tNow = 50;

// 輸出瞬時失效率與可靠度
console.log(`[t = ${tNow}h] 瞬時失效率：${hazard(tNow).toFixed(6)}`);
console.log(`[t = ${tNow}h] 可靠度：${reliability(tNow).toFixed(6)}`);

// 計算在 p 失效率下之壽命 t_p（此處 p = 0.01 → 99% 可靠度）
const p = 0.01;
const tP = scale * Math.pow(-Math.log(1 - p), 1 / shape);
console.log(`預估最大壽命 t_p：${tP.toFixed(2)} h`);

console.log("可將參數儲存至刀具資料檔，以供後續分析使用：");
console.log(`shape: ${shape}`);
console.log(`scale: ${scale}`);