在不同的語境下的「可能（may）」具有多種解讀，描述性的（知識論）「可能」非常令人困惑。

「可能是 $\phi$（it may be, it might be, it is possible）」的標準語義，表達的是在說話者不知道 $\sim \phi$ 的情況下的某事情。因此，摩爾說：「我可能沒有坐著……」的意思是「不確定我坐著」或「我不知道我坐著」。

更複雜的版本允許認識者和/或檢驗 $\phi$ 的訊息變化：

• 對 A 來說，$\phi$ 可能為真，當且僅當 A 所知道的不能明顯推導出 $\sim \phi$。
• 對 A 來說，$\phi$ 可能為真，當且僅當（1）相關社群中沒人知道 $\phi$ 是假的，並且（2）相關社群中的成員沒有相關方法來知道 $\phi$ 是假的。

標準語義有其正確的地方，但也有錯誤的地方：

1. 主題錯誤：當我說「Bob 可能在他的辦公室」，我談論的是 Bob 和他的辦公室，而不是我的訊息程度，我擔心的是他在哪，而非我不知道他在其他地方。
2. 真值條件可能太弱：光是我不知道 $\sim \phi$ 無法令可能 $\phi$ 為真。
3. 對說話者而言，真值條件可能太強：有些說話者缺乏的關於 $\sim \phi$ 的證據可能存在。
4. 過於知識論：「可能」可以用在其他語境，它可能展現的是非知識論的內容。
5. 在邏輯上有個（看似的）悖論。假設 $\phi$ 與所有相關訊息是一致的，因此，如果 $\phi$ 蘊含 $\psi$，「$\phi$ 可能為真」應該蘊含「$\psi$ 可能為真」。例如，「Bob 可能在他的辦公室」應該蘊含「Bob 可能在他的辦公室或在鴉片窟」。然而，「Bob 可能在他的辦公室或在鴉片窟」提出了更強的主張。許可的狀況也有類似的困惑：為什麼「你可以去或者留」似乎蘊含了你可以做你想做的？
6. 「$\phi$ 且可能 $\sim \phi$」在邏輯上不融貫：標準語義的優點是解釋了「$\phi$ 且可能 $\sim \phi$」的悖論性，但這是指「$\phi$ 但我不知道 $\phi$」的摩爾悖論的（通常認為的）不可斷言性。實際上，我依然能在一些情境下假設這個語句，這要如何解釋？（Yablo 將這歸給 Seth Yalcin。）

為了解決知識論模態詞問題，有人提出動態語義學：「可能 $\phi$」的意義不在於其真值條件，而在它對語境或共享資訊的影響。

Frank Veltman 的預設語義學（default semantics）表示，若「可能 $\phi$」是在資訊狀態 $S$ 中的表述，若 $S$ 與 $\phi$ 一致，會返回相同的資訊狀態 $S$，如果 $S$ 與 $\phi$ 不一致，則返回空資訊狀態（null information state）。

Yablo 指出，這兩部分看起來都與「可能」的使用方式不符合：

• 考慮「可能 $\phi$」在 $S$ 與 $\phi$ 不一致時返回空狀態的想法。

假設大家都明白 John、Paul、George 和 Ringo 會參加聚會。然後 Yoko 跑進來說「Ringo 可能不能來」。Ringo 不能來與 John、Paul、George 和 Ringo 都會在那裡是不一致的，我們所有的資訊都被摧毀了。但直覺上，當我們得知 Ringo 可能不參加時，有關 John、Paul 和 George 會參加聚會的資訊仍然存在。

• 考慮「可能 $\phi$」在 $\phi$ 與 $S$ 一致時返回 $S$ 的想法。

John、Paul、George 和 Ringo 參加聚會與 Ringo 或 Elton John 缺席是一致的；因為可能是 Elton John 缺席。然後 Yoko 跑進來說「Ringo 或 Elton John 可能不參加」，我們就不會假設披頭士都會在。我們的共享資訊被削弱為：John、Paul 和 George 會參加聚會。

從兩個例子來看，「可能 $\phi$」在資訊狀態 $S$ 中表達時，可能削弱 $S$ 到一個較弱的資訊狀態 $S'$；並且無論 $\phi$ 與 $S$ 一致還是不一致，它都能產生這種效果。

如果以世界集來建模資訊狀態，那麼「可能 $\phi$」的效果是添加額外的世界。但會添加哪些世界？

David Lewis 在 “A Problem about Permission” 討論過類似的問題：

Lewis 描述了一個簡單的語言遊戲。玩家包括主人、奴隸和旁觀者，儘管我們會忽略旁觀者。

主人向奴隸發出命令和許可，從而縮小和擴展 Lewis 所稱的許可範圍（sphere of permissibility），即奴隸該如何行為的世界集合。在這個遊戲中，奴隸唯一的目的是按照應該的方式行為。這意味著，去行為，以使現實世界位於許可範圍內。然而，如果奴隸不知道範圍在哪，他無法保持在範圍內。

範圍演變如下：

當遊戲開始時，所有世界都是被允許的。現在主人開始發出命令和許可。我們的工作是找出一個函數，將給定的一系列命令（$! \phi$）和許可（$\text{i} \phi$）映射到相應的許可世界集合。

命令對許可範圍的影響規則為：

• $! \phi$：$S \rightarrow S \cap |\phi|$

或表達為：

• (C) $! \phi(S) = S \cap |\phi|$

許可的影響初步來看可能是這樣想：

• $\text{i} \phi$：$S \rightarrow S \cup |\phi|$

或表達為：

• (P) $\text{i} \phi(S) = S \cup |\phi|$

從左到右的包含關係難以反駁，但從右到左所需要的原則卻明顯錯誤。這裡的原則是：

• (??) 許可 $\phi$ 使所有 $\phi$ 世界被允許。

但 Lewis 解釋：假設奴隸被命令每天都搬石頭，但星期四主人對奴隸說「$\text{i}$ 明天不用工作」。他因此允許了休假，卻不包括休息到週日的休假。(??) 允許了太多。它只該允許「一些」，但至於是哪些，這裡會需要一些不需明說的條件。

因此，這裡必須一些規則和原則來捕捉對許可如何運作的共同理解。

奴隸可以休息到週日的規則 R 有什麼問題？Lewis 列出五個答案：

1. R 允許了超出必要的世界。這回答的問題在於這似乎不是主要問題。
2. R 允許了比必要的更遠的世界。這問題太嚴苛了，這會讓奴隸的休假可能必須做和他平時工作更類似的事情。取消的命令會影響允許的世界，Yablo 將這稱作乾淨取消問題（clean cancellation requirement）。
3. R 允許了比必要的更不允許的世界。這會讓許可的範圍被因為之前的命令而受限。這是乾淨取消問題的另一個版本。
4. R 允許了比必要更讓主人不愉快的世界。這會讓許可的範圍被之前的命令扭曲。這還是乾淨取消問題的一個版本。
5. R 允許了違反更多命令的世界。這需要進一步說明。

依照答案 5。建議是，許可 $\phi$ 的效果應該是使禁止 $\phi$ 的命令失效，但同時保留其他命令。允許星期六休息的更新規則的問題，在於它使更多的命令無效。將此更新規則稱為剩餘規則，將 $S^+$ 定義為滿足當 $\phi$ 不一致命令被取消時剩下的命令的世界集合。

Lewis 不喜歡這規則的原因如下。為了應用該規則，我們需要一個命令列表 $\psi_1, \ldots, \psi_k$。一個世界如果符合所有命令即被認為是允許的，即：

• $S = |\psi_1| \cap |\psi_2| \cap \ldots \cap |\psi_k|$

假設與 $\phi$ 不相容的命令是 $\psi_{j+1}, \psi_{j+2}, \ldots, \psi_k$，則新的範圍 $S^+$ 是：

• $S^+ = |\psi_1| \cap |\psi_2| \cap \ldots \cap |\psi_j|$

但是，初始命令集合應該從哪裡來？我們似乎需要做逆向工程，重新構造命令包來定義當前的許可範圍。但 $S$ 和定義 $S$ 的命令間的關係是多對一的，許多命令包都可以導致相同的許可範圍，而奴隸該用哪個命令包？這問題重要是因為允許 $\phi$ 對 $S$ 的影響會因選擇不同的隱含命令 $\psi_i$ 而不同。

假設 $S$ 是奴隸從周一到周日每天工作的世界。奴隸可能認為在給予他星期五休息之前，有效的命令是

• $\psi_1$：奴隸周一搬石頭。
• $\psi_2$：奴隸周二搬石頭。
• $\psi_3$：奴隸周三搬石頭。
• $\psi_4$：奴隸周四搬石頭。
• $\psi_5$：奴隸周五搬石頭。
• $\psi_6$：奴隸周六搬石頭。
• $\psi_7$：奴隸周日搬石頭。

這裡唯一與「奴隸星期五休息」不一致的命令是「奴隸周五搬石頭」。暫停這一命令，保留其他天的工作命令。顯然，這樣做的結果是，奴隸並未被允許休其他天，這是預期的結果。

但奴隸也可能認為隱含命令是

• $\chi_1$：奴隸平日搬石頭。
• $\chi_2$：奴隸周末搬石頭。

現在，不一致的規則，即在當前假設下被取消的規則，是「奴隸平日搬石頭」。但這樣許可範圍擴展到包括所有奴隸在周末工作的世界。這便不太對。

Lewis 的反對意見簡而言之是，隱含命令對剩餘規則來說太不受約束。

Yablo 指出，Lewis 可能是對的，但還有一些他忽略的約束問題，要再更極端的方式下提出才會顯示出來。有些更嚴重的隱含命令的誤會。

一種是，所有命令都和 $\phi$ 不一致：

• $\theta_1$：奴隸每周早上搬石頭。
• $\theta_2$：奴隸每周下午搬石頭。

一種是，所有命令都和 $\phi$ 一致：

• $\sigma_1$：如果奴隸在任何下午搬石頭，那每個早上搬石頭。
• $\sigma_2$：如果奴隸在每個早上搬石頭，那每個下午搬石頭。
• $\sigma_3$：奴隸在某個下午搬石頭。

這三個命令沒有一個和許可不一致。

Yablo 認為，可以透過這些荒謬結果來指出命令列表的合理約束。說一個命令列表是合理的，若它以剩餘規則的運行結果滿足 (p1)–(p3)：

• (p1) 許可會擴展（不限縮）範圍。
• (p2) 許可 $\phi$ 只使 $\phi$ 世界被允許。
• (p3) 許可 $\phi$ 使一些 $\phi$ 世界被允許。

Yablo 證明（見附錄）：

如果 $S$ 是由合理的命令列表定義的，那麼 $S = |\sim \phi| \cap |\psi|$ 對某些 $\psi$ 成立。等價地，任何合理的命令列表的形式是（至多等價）「你不得 $\phi$」與「你必須 $\psi$」。

而每當有 $\phi$ 的許可時，初始命令列表由兩個命令組成：

• 一個說明（精確地）不做 $\phi$ 的命令。
• 一個允許做 $\phi$ 的命令。

重劃範圍的任務是，我們要拋棄「不做 $\phi$」的命令，再形成由剩下的命令允許的世界集合。

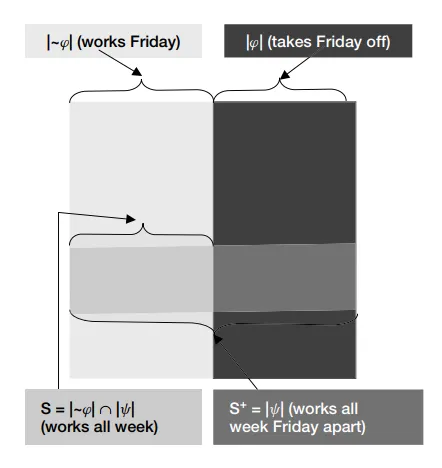
上圖是任務的圖解：

• $|\phi|$ 區域：奴隸星期五休息的世界，他被允許這樣做。
• $|\sim \phi|$ 區域：奴隸星期五工作的世界，他本來的命令。
• $S$ 區域：那是奴隸每天工作的最初允許的世界集合。
• 我們的任務：將 $S$ 區域外推到 $|\sim \phi|$ 區域外，得到主人取消工作星期五命令後的世界集合 $|\psi|$。

Yablo 認為，這個圖可以幫助我們理解 $S = |\sim \phi| \cap S^+$ 的含意。此外也能理解，要將 $S$ 擴展到 $\phi$ 區域，原則上不只一種方法，還有許多可能的外推法（extrapolation）。最後這能看出，有些外推方法要比其他方法更加自然，更能擺脫乾淨取消問題。

乾淨取消問題歸結是，一個命題（在這裡是 $|\psi|$）如何能「自由於」另一個命題（$|\sim\phi|$）。命題 A 是 B 自由的，當且僅當：

• 在 A 為真的世界裡，它的為真原因與 B 為假相容；
• 在 A 為假的世界裡，它的為假原因與 B 為真相容。

Yablo 提出的許可更新規則如下：

(UR , !)

假設 $S$ 是當前的許可範圍，且在 $S$ 世界中沒有 $\phi$ 成立。$S^+ = S + \text{i} \phi$ 當且僅當滿足四個條件：

1. 差異（Difference）：$S^+ - S$ 非空
2. 等同（Equality）：$S = |\sim\phi| \cap S^+$
3. 自由（Freedom）：$S^+$ 是 $|\sim\phi|$ 自由的
4. 良好（Goodness）：其他滿足 D、E 和 F 的候選者「不太好」

接下來 Yablo 探討 Lewis 的主人-奴隸遊戲的知識論類比。他提出的新遊戲：

玩家是老師和學生，許可範圍改成可信範圍。學生不斷調整他的理論以適應可信變化。當老師說「$\psi$ 是這樣的」時，可信範圍收縮；當老師說「$\phi$ 可能是這樣的」時，範圍擴展。

Yablo 指出可信範圍的更新規則如下：

(UR, $\Diamond$)

假設 $S$ 是當前的可信範圍，且在 $S$ 世界中沒有 $\phi$ 成立。$S^+ = S + \Diamond \phi$ 當且僅當滿足四個條件：

1. 差異（Difference）：$S^+ - S$ 非空
2. 等式（Equality）：$S = |\sim\phi| \cap S^+$
3. 自由（Freedom）：$S^+$ 是 $|\sim\phi|$ 自由的
4. 良好（Goodness）：其他滿足 D、E 和 F 的候選者「不太好」

Lewis 指出有一種命令可能要特殊處理：命令哪些事情不可允許。他的解決方法是：每當 $\phi$ 是不可允許的，命令 $\phi$ 是由默認的允許 $\phi$ 所前置的，許可範圍依此而相應演變。Yablo 認為也可以引入類似的操作方法：每當 $\phi$ 是可信的，而「可能是 $\phi$」是對未說出的斷言 $\sim\phi$ 的回應。

正如允許然後命令 $\phi$ 可以改變許可範圍一樣，禁止然後允許 $\phi$ 也可以改變許可範圍。數學上，沒有任何理由期望 $S^{−+} = \text{i} \phi (! \sim\phi(S))$ 會只是 $S$，事實上，根據自由條件，$S^{−+}$ 是 $| \sim\phi |$ 自由的。

現在回到標準語義學（Standard Semantics，簡稱 SS）的問題。

第一個問題是 SS 給予「可能 $\phi$」的主題是錯誤的。當前我們將「可能 $\phi$」解釋為撤回或取消對 $\sim\phi$ 的斷言的工具。如果 $\phi$ 的主題在否定和未否定的情況下一樣，且 $\sim\phi$ 的主題在撤回和斷言的情況下一樣，那「可能 $\phi$」的主題就與 $\phi$ 一樣。

第二個問題是 SS 分配的真值條件太弱。假設「可能 $\phi$」不是一個事實陳述，而是一個「取消命令」：試圖撤銷或反轉對 $\sim\phi$ 的斷言，而非表明 $\sim \phi$ 不能在背景之中。

第三個問題是，真值條件太強。對於取消理論來說，可以表明，說話者斷言陳述時所需要的自我約束，取決於他當下的擔憂有多強。

第四個問題是 SS 過於知識論化。但目前可以說，有些可能斷言是為了表達對其他斷言的取消。

第五個問題：在取消理論的脈絡中，「更強的聲明」是一個取消更多的聲明。所以只要表明 $\Diamond\phi$ 只取消 $\sim\phi$，而 $\Diamond(\phi \lor \psi)$ 會取消 $\sim\phi$ 和 $\sim\psi$。

假設 $S$ 是蘊涵 $\sim\phi$ 和 $\sim\psi$ 的可信範圍。「可能」的更新規則告訴我們 $S + \Diamond(\phi \lor \psi)$ 是 $S$ 的超集 $S^+$，且 $S^+$ 是 $\sim(\phi \lor \psi)$ 自由的。

根據自由的定義，意思就是：

• (#) $S^+$ 為假的理由與 $\sim(\phi \lor \psi)$ 為真相容，即與 $\phi$ 和 $\psi$ 共同為假相容。

那麼，使 $\phi$ 或 $\psi$ 為假的事實不會使 $S^+$ 為假。但若 $S^+$ 蘊涵 $\sim\phi$，那麼使 $\phi$ 為真的事實可能便會使 $S^+$ 為假；如果 $S^+$ 蘊涵 $\sim\psi$，情況也是類似。因此 $S^+$ 不蘊涵 $\sim\phi$，也不蘊涵 $\sim\psi$。這意味著 $\Diamond(\phi \lor \psi)$ 的效果是同時取消 $\sim\phi$ 和 $\sim\psi$。這解釋了為什麼「可能是 $\phi$ 或 $\psi$」暗示「可能是 $\phi$」和「可能是 $\psi$」。

第六個問題是，SS 解釋不了為什麼「$\phi$ 且可能 $\sim\phi$」在條件句的前件中不融貫，但「$\phi$ 且我/我們不知道 $\phi$」卻沒這個問題。問題並不在於沒有世界能同時滿足 $\phi$ 和 $\Diamond \sim\phi$ 的要求，而是，沒有世界規範可以既要求 $\phi$ 又不要求 $\phi$。

然後是更新語義學（update semantics）未充分解釋為何允許 Ringo 可能不去聚會會保留 John、Paul 和 George 將參加的資訊的問題。

取消理論說，只有與 Ringo 參加聚會相關的先前斷言才會被取消。「John、Paul 和 George 將參加」是與「Ringo 參加」無關的，因為使第一個為真（假）的事實不與使第二個為假（真）的事實衝突。

對更新語義學的第二個問題是，更新語義學告訴我們在資訊狀態 $S$ 中的表達 $\Diamond\phi$ 沒有影響，除非 $S$ 與 $\phi$ 不一致。假設 $S = \{\sim\chi\}$ 且 $\phi = \Diamond(\chi \lor \psi)$。 $\chi \lor \psi$ 與 $\sim\chi$ 一致，所以 $S + \phi$ 應該是 $S$。

但 $\Diamond(\chi \lor \psi)$ 通常蘊涵 $\Diamond\chi$ 和 $\Diamond\psi$。知道 $\chi$ 可能為真會取消我們之前關於 $\sim\chi$ 的任何資訊。這是 $S + \phi$ 是 $S$ 的真子集的情況，即便 $\phi$ 和 $S$ 是一致的。

取消理論如何處理這情況？

$S + \Diamond\phi$ 是 $S$ 中 $\sim\phi$ 的自由部分。但從 $\phi$ 與 $S$ 一致，得知 $S$ 不蘊涵 $\sim\phi$，但我們不能推斷 $S$ 自由於 $\sim\phi$。不蘊涵 $\chi$ 是一個比自由於 $\chi$ 弱得多的性質。

例子是，$\chi \lor \psi$ 與 $\sim\chi$ 和 $\sim\psi$ 一致，而它們也不蘊含 $\chi$ 和 $\psi$，但選言並不對選言項自由。

David Efird 回應 Stephen Yablo

考慮：

• (1) 你可能去看足球賽或坐火車。
• (2) Lewis 可能去看足球賽或坐火車，但我不知道哪一個。
• (3) 你可能去看足球賽或坐火車，但我不知道哪一個。

在語句 (1) 中，「可以」的許可意義似乎是由「你」的出現強制的，而在語句 (2) 中，「可以」的知識論意義似乎是由「但我不知道哪一個」的出現強制的。但語句 (3) 中，「你」似乎強制了「可能」的規範意義，但「我不知道哪一個」的出現似乎引入了額外的知識論意義。

存在不可化約的選言許可

Efird 指出，存在著不可化約的選言許可，有一些選言許可既不蘊涵選言許可也不蘊涵連言許可。

考慮以下語句：

• (1) 你可能去看足球賽或坐火車。
• (4) 你可能去看足球賽。
• (5) 你可能坐火車。
• (6) 你可能去看足球賽和你可能坐火車。
• (7) 你可能去看足球賽或你可能坐火車。

句子 (1) 似乎有兩種解讀。

在第一種解讀中，(1) 蘊涵 (4) 和 (5)，因此也蘊涵 (6)，但 (4) 和 (5) 都不蘊涵 (1)。在這種解讀中，選言許可蘊涵許可的連言，但沒有一個連言項蘊涵選言許可。

在第二種解讀中，(1) 被解讀為 (7)。(4) 和 (5) 都蘊涵 (1)，但 (1) 既不蘊涵 (4) 也不蘊涵 (5)。

如果將「但我不知道哪一個」附加到第一種解讀，我們會得到：

• (8) 你可能去看足球賽和你可能坐火車，但我不知道哪一個。

(8) 是語用矛盾的例子，即 Seth Yalcin 的摩爾悖論的版本：「$\phi$ 且可能是 $\sim\phi$」：

• (8$^*$) $(PA \& PB) \& (\Diamond \neg PA \& \Diamond \neg PB)$

其中 $P$ 表示規範性可能運算符，$A$ 和 $B$ 表示語句的語義字母。$\Diamond$ 表示知識論可能運算符。這在邏輯上等價於摩爾-Yalcin 悖論的兩個實例的連言：

• (8$^{**}$) $(PA \& \Diamond \neg PA) \& (PB \& \Diamond \neg PB)$

因此，如果把 (3) 讀成 (8) 會造成悖論。

第二種解讀則報告了在某許可集中的某許可在起作用，但不知道是哪個許可在起作用。「我不知道哪一個」被隱含地添加到 (1)，來獲得 (3)。

因此第二種解讀即是：

• (9) 你可能去看足球賽或你可能坐火車，但我不知道哪一個。

形式上是：

• (9$^*$) $(PA \lor PB )\& (\Diamond \neg PA \& \Diamond \neg PB)$

蘊含：

• (9$^{**}$) $[(PA \& \Diamond \neg PA) \lor (PB \& \Diamond \neg PA)] \& [(PB \& \Diamond \neg PB) \lor (PA \& \Diamond \neg PB)]$

因此，(3) 不能被解釋為 (8) 或 (9)，即 (3) 中的選言許可必須被解釋為不可化約的選言許可，它既不蘊涵許可的選言也不蘊涵許可的連言。

不可化約的選言許可不遵守自由條件

根據 Yablo 的語義學，句子 (1) 蘊涵句子 (6)，但當「但我不知道哪一個」被附加到 (1) 時，這蘊涵似乎受到限制，否則會導致摩爾-Yalcin 悖論。

問題在於，Yablo 的許可更新規則似乎在 (3) 這樣的情況下失效。「自由條件」在這情況下似乎不成立。

該條件要求 $S^+$ 是 $\neg(A \lor B)$-自由的。這意味著 $S^+$ 是 $(\neg A \& \neg B)$-自由的。但不可化約的選言許可恰好無法如此。

如果 $S^+$ 是 $(\neg A \& \neg B)$-自由的，那麼，$S^+$ 為真的理由與 $(\neg A \& \neg B)$ 相容。但現在，$S^+$ 為真的地方是 $P(A \lor B)$ 為真的地方，而其為真的原因，在像 (3) 這樣的情況下，部分來自於不確定性，這種不確定性在許可範圍內產生了不完整的、非最大化的世界。這就是選言許可在上述定義的意義上不可化約的表現。因此，$S^+$ 為真的原因不與 $(\neg A \& \neg B)$ 的為假、即 $(A \lor B)$ 為真相容，因為這需要確定性。而不確定性導致 $S^+$ 不是 $(\neg A \& \neg B)$-自由的。