基本術語定義

$\Gamma$ 全立基（fully grounded）$x$。

定義偏立基

$y$ 偏立基 $x$ ${=}_{df}$ 存在 $\Gamma$ 使得 $y \in \Gamma$ 且 $\Gamma$ 全立基 $x$。

公理

全非反身性。對於任何 $\Gamma$，$\Gamma, x$ 非全立基 $x$。

全切消。若 $y, \Gamma$ 全立基 $x$，且 $\Delta$ 全立基 $y$，則 $\Gamma , \Delta$ 全立基 $x$。

透過這兩個公理，我們可以推出 偏非反身性、全對稱性、偏對稱性、全遞移性、偏遞移性。

定義立基結構

立基結構。$\Gamma$ 構成一個立基結構（grounding structure） ${=}_{df}$ 存在 $x$ 和 $y$，$x, y \in \Gamma$，使得 y 偏立基 x。

立基鏈。$\Gamma$ 構成一個立基鏈（grounding chain） ${=}_{df}$ (i) $\Gamma$ 構成一個立基結構，並且 (ii) 對於所有 $x$ 和 $y$，$x, y \in \Gamma$，要嘛 $x$ 偏立基 $y$，要嘛 $y$ 偏立基 $x$，要嘛 $x = y$。

無限後退與循環

何謂立基的無限後退？T. Scott Dixon 認為，那就是存在一個包含 無限後退立基鏈 的立基結構。

無限後退立基鏈。$\Gamma$ 構成一個 無限後退立基鏈 ${=}_{df}$ (i) $\Gamma$ 構成一個立基鏈，並且 (ii) 對於所有 l$x$（$\in \Gamma$），存在一個 $y$（$\in \Gamma$），使得 $y$ 偏立基 $x$。（Rabin 與 Rabern 2016:371）

不難看出我們的公理系統不允許循環。要允許循環的話，我們要拒絕偏遞移性或是偏反身性。這意味著我們必須放棄公理之一。我們或許會優先考慮保留非反身性。如果是這樣，那在許多討論域中，由於偏遞移並不成立，我們可以嘗試修改本來的定義來避免問題：

立基鏈。$\Gamma$ 構成一個立基鏈（grounding chain） ${=}_{df}$ (i) $\Gamma$ 構成一個立基結構，並且 (ii) 對於所有 $x$ 和 $y$，$x, y \in \Gamma$，要嘛 $x$ 偏立基+ $y$，要嘛 $y$ 偏立基+ $x$，要嘛 $x = y$。

「偏立基+」代表偏立基的遞移閉包：

偏立基遞移閉包。在集合 $S$ 上的偏立基的遞移閉包是滿足「對於所有 $S$ 中的 $x$、$y$ 和 $z$，(i) 如果 $y$ 偏立基 $x$ 則 $xRy$，(ii) 如果 $xRy$ 且 $yRz$ 則 $xRz$ 」的 $R$ 中最小的。

根據新的立基鏈的定義，循環立基鏈可以這樣定義：

循環立基鏈。$\Gamma$ 構成一個 循環立基鏈 ${=}_{df}$ (i) $\Gamma$ 構成一個立基鏈，並且 (ii) 在 $\{ \Gamma \}$ 上的偏立基遞移閉包有反身性。

我們的循環（cyclic）符合無限後退立基鏈的定義（雖然循環是否算是無限後退是有爭議的）。

無限後退立基

先考慮形上學的基礎論：

形上學基礎論（最初）。 基礎實體的底層必須存在，它為其他所有實體立基。

所謂的「基礎（foundamental）」可以這樣定義：

基礎。 $x$ 是基礎的 ${=}_{df}$ 沒有事物立基 $x$。

類似基礎論的支持者包括 Jacek Brzozowski（2008）、Ross Cameron（2008）、Kit Fine（2010: 105）、Jonathan Schaffer（2010: 37, 62, 2016: 95）和 Karen Bennett（2011）。

這種理論在目前的討論中可以稱作良立基性（well-groundness）。根據 Scott Dixon （2016）、Gabriel Rabin 與 Brian Rabern（2016），有這些不同的版本的公理可補充來滿足良立基性：

無無限後退鏈。 沒有無限後退鏈。

無最大無限後退鏈。 所有的最大立基鏈都不是無限後退鏈。

無弱最大無限後退鏈。 所有的弱最大立基鏈都不是無限後退鏈。

全基礎。 對於所有非基礎實體 $x$，有一個基礎實體集合 $\Gamma$（$x \in \Gamma$）使得 $\Gamma$ 全立基 $x$。

以下是上述術語的定義：

最大立基鏈。 $\Gamma$ 是一個 最大立基鏈 ${=}_{df}$ (i) $\Gamma$ 構成一個立基鏈，並且 (ii) 沒有事物偏立基 $\Gamma$ 的所有 $x$。

弱最大立基鏈。 $\Gamma$ 是一個 弱最大立基鏈 ${=}_{df}$ (i) $\Gamma$ 構成一個立基鏈，並且 (ii) 不存在全立基 $\Gamma$ 的所有有限區段中的所有 $x$ 的 $\Delta$。

有限區段。 $\Delta$ 構成 $\Gamma$ 的有限區段 ${=}_{df}$ (i) $\Gamma$ 構成一個立基鏈，(ii) $\Delta$ 非空， (iii) $\Delta$ 包含於 $\Gamma$，並且 (iv) 所有在 $\Gamma$ 中但不在 $\Delta$ 中的 $x$，由 $\Delta$ 中的所有 $y$ 偏立基。

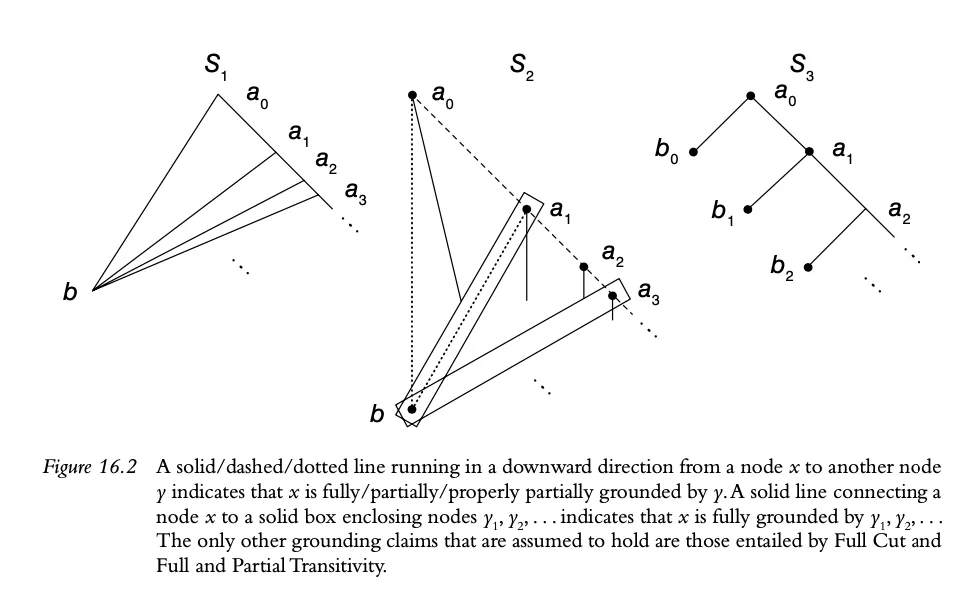
Dixon、Rabin 和 Rabern 認為，全基礎公理是最可信的。良基性即便可以在一定程度上避免某些無限後退，但全基礎公理依然最符合基礎論者的精神。以下有 $S_1$、$S_2$ 和 $S_3$ 三個圖示。Dixon 等人認為，$S_1$ 和 $S_3$ 都滿足基礎論者的需求，但 $S_2$ 不滿足，全基礎 滿足這樣的需求。 無無限後退鏈 錯誤地剔除掉了 $S_1$ 和 $S_3$。 無最大無限後退鏈 錯誤地允許了 $S_2$，並且剔除了 $S_3$。 無弱最大無限後退鏈 剔除了 $S_3$。

假若如此，形上學的基礎論可以更精準地這樣表示：

形上學基礎論（最終）。 對於所有非基礎實體（entity） $x$，存在一些基礎實體 $\Gamma$（$x \in \Gamma$）使得 $\Gamma$ 全立基 $x$。

如果是這樣，即便是以基礎論的觀點來看，無限後退依然是可能的，只要它是良立基的。那如果不是呢？無限後退依然是可能的嗎？基礎論者會說不行，但無限論者（infinitist）會說可以：

最小的形上學無限論。 至少有一個這樣的無限後退立基鏈：在裡面至少有一個實體，它不由任何基礎實體（或集合）所全立基。

Matteo Morganti 提倡了更強的版本，主張無限論的立場應該是「在立基域中的 所有 實體，都位於一個無限後退立基鏈的頂端。」（2014, 2015）

非良立基的無限立基鏈的否定

論證一：Shaffer（2010, 2016）

實在是一種這樣的質：在立基域中的所有實體，必須在這個質上被完全度量，並且單單透過立基便可以從這樣的一個實體傳遞到另一個實體。也就是說，一個實體 $x$ 有完全度量的相關的質，若且唯若，要嘛 (i) $x$ 是基礎的，要嘛 (ii) $x$ 由其他該質有完全度量的實體所全立基。

論證二：Cameron（2008）

其他事物相同的情況下，我們應該避免理論中有無限後退鏈的解釋關係鏈。考慮一個我們想要解釋的現象集合 $P$，假設有兩個理論，$T_1$ 和 $T_2$，$T_1$ 以單一個基礎實體 $x$ 提供了 $P$ 完整的解釋，而 $T_2$ 以一個無限後退的事實鏈 $f_1, f_2, ...$ 來解釋 。我們通常會覺得 $T_1$ 是更好的理論。

論證三：Bliss（2019）

一旦每個存在的非基礎實體都被提供了完整的解釋，有人可能會認為總是有某些東西需要被解釋。這樣的情況顯示全基礎的模型是錯的。但那些東西之所以還需要被解釋，就是因為有一些非基礎實體存在，而只有在以基礎實體來解釋它們的時候，解釋才算是被提供了。Bliss 將這稱作「外在性假設」：沒有非基礎實體可以解釋任何非基礎實體。

非良立基的無限立基鏈的肯定

論證一：Shaffer（2003）、Tahko（2014）

如果後退項是「無聊的」或是「重複的」，那麼無限後退鏈就是可能的。Shaffer 和 Tahko 所謂的無聊的無限後退結構的無聊部分是基礎的隨附基底。一旦決定了有一個區段在基底中不斷重複的定律，就沒有更多有意義的科學工作需要被完成。Shaffer 認為這種理論並沒有比基礎論的圖示更差。

論證二：Morganti（2014, 2015）

實體不會從立基者轉換成被立基者，而是實體從一個（或多個）從給定實體開始的無限鏈中突現出來（類比 Peter Klein（2007）對於知識證成的想法）。在 Morganti 的這種想法裡面，立基的關係項的存在不依賴於是不是有任何人能表徵它。

論證三：Raven（2016）

一個實體是基礎的，只是因為它在這個情況下是基礎的。一個實體是不可消除的因此是基礎的，這個不可消除的意思是「少了它，實體就不能被完全描述」。這種看法雖然沒有直接論證非良立基的無限立基鏈存在，但由於缺少了絕對的解釋上的基礎物體，無限論者便可以主張，所有立基鏈都不算有良立基性。

論證四：Bohn（2018）

部分立基全體。 必然地，對於所有 $x$ 和 $y$，如果 $x$ 是 $y$ 的恰當部分，那麼 $x$ 偏立基 $y$。 全體立基部分。 必然地，對於所有 $x$ 和 $y$，如果 $x$ 是 $y$ 的恰當部分，那麼 $y$ 偏立基 $x$。

因此一個物體可以既是黏合的（gunky）也是雜堆的（junky）（他稱作「hunky」）。在這種觀點下，形上學的基礎論 實然地 不是對的。

論證五：Bohn（2018）

基礎事實沒有辦法回答它們為何存在的問題，但這應該要有理由（Bohn 認為）。他的假設是「形上學的充足理由原則（MPSR）」：所有事實都有形上學的解釋。

Bohn 認為，即便 MPSR 不對，要違反它也是必須要有好理由。