主要論證目標：

• 模態先驗論是有問題的：如果模態是豐富的，那先驗反思不是可靠的指引。如果模態是稀少的，先驗反思不會是可能性的標記（mark）。
• 模態需要怎樣的豐富性（bounty），取決於如何最好地對思維系統化。模態先驗論應該取決於對我們最深刻哲學的關注。

關於先驗反思和可能性信念的辯論結構，有三個問題：

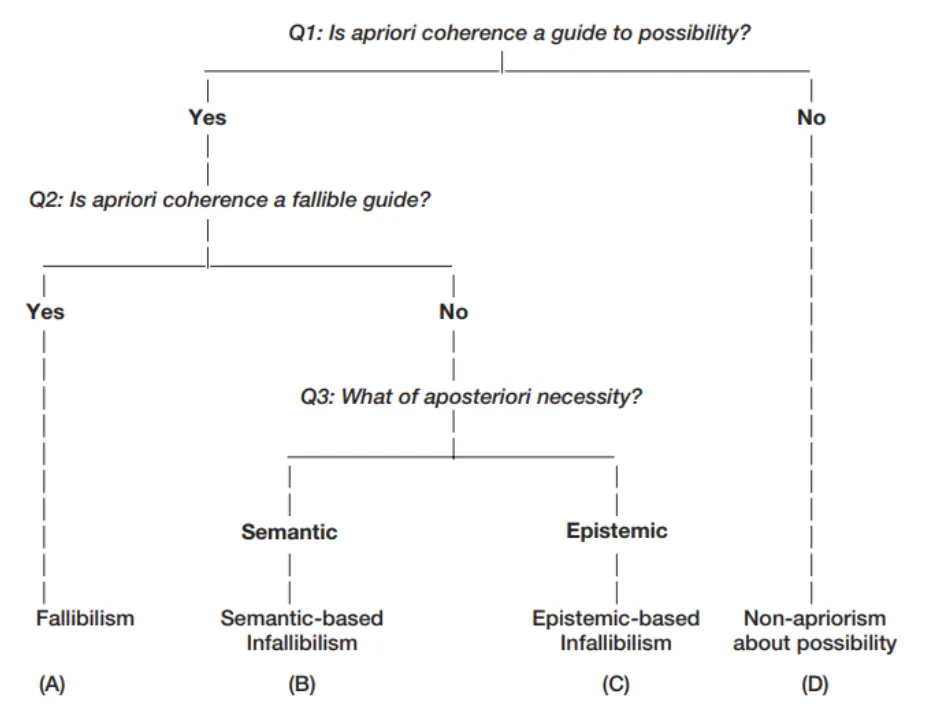
• (Q1) 先驗融貫性是可能性的指引嗎？聲明的先驗特徵是可能性的標記。如果一個聲明能經得起先驗反思，他是可能的。反之亦然。先驗反思是可能性的標記。先驗可錯論：先驗反思是可能性的標記，但它是可錯的。
• (Q2) 先驗融貫性是可能性的可錯指引嗎？
• (Q3) 後驗必然性？以語義學為基礎，不可錯論似乎能讓我們更容易理解後驗必然性的直覺。

根據三個問題，可以有四種觀點。(A)-(C) 是三種先驗論：

• (A) 可錯論
• (B) 語義學基礎的不可錯論
• (C) 知識論基礎的不可錯論
• (D) 非先驗論

模態的形上學和邏輯學的兩種標籤，都暗示模態充滿先驗性、具有邏輯的開放性。Jackson 想考慮的是真正的模態（genuine modality），他定義為「最絕對的實在模態空間（the most absolute realistic modal space）」，這概念可以可能性或必然性來解釋：

• 真正可能的 $\phi$ 是獨立於心靈和語言的事實，而 $\phi$ 能發生。實在論是真正可能性的組成部分，並且具有弱性：只要有一種實在論的意義上 $\phi$ 能發生，$\phi$ 就是真正可能的。
• 真正必然的 $\phi$ 是獨立於心靈和語言的事實，而 $\phi$ 能發生。實在論是真正可能性的組成部分，並且具有強性：當 $\phi$ 是真正必然的，它在任何實在論意義上都是必然的。

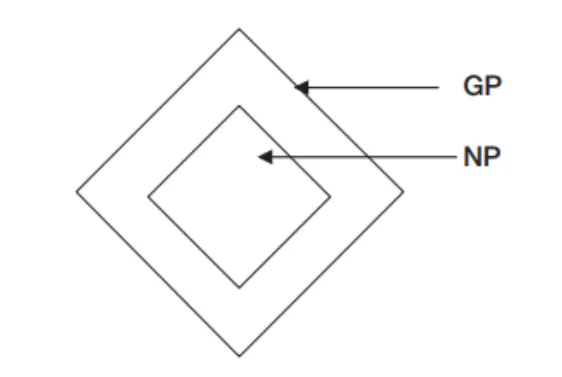
自然律可能性（NP）包含所有自然律上可能的聲明，真正可能性（GP）包含所有真正可能的聲明。真正可能性是最弱的現實模態空間，所以所有實在的菱形都嵌入在真正可能性（GP）內。圖示如下：

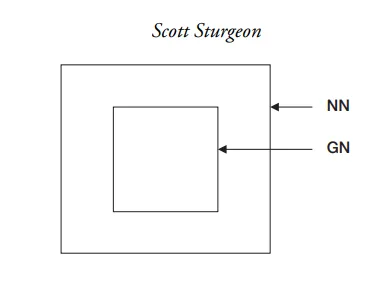
真正必然性（GN）包含在所有實在必然性內。例如，它包含在自然律必然性內；所以如果有真正適真的自然律必然性，那麼真正必然性（GN）就嵌入在自然律必然性（NN）內。圖示如下：

基於知識論的觀點

我們可以用下面這個表達式來表示「$\phi$ 是表面上先驗融貫的（prima facie apriori coherent）則 $\phi$ 是可能的」的最樸素先驗不可錯論：

• (p) $\text{pfac}(\phi) \rightarrow \Diamond \phi$

(p) 是錯的，因為先驗反思可以自我修正。真正的不可能性通常是表面先驗融貫的。

改成極限融貫（limit coherent）的概念：我們允許最大限度的思考時間、專注、記憶、計算能力，在純粹的知識論維度中最大化智力。表達為極限先驗的不可錯論：

• (l) $\text{lim}(\phi) \rightarrow \Diamond \phi$

Kripke 反駁了極限融貫與真正模態視同一見識：在先反思的極限情況下融貫的東西可以是真正不可能的，透過非模態事實的先驗反思可以表面這件事。

設 K 是 Mark Twain 是 Sam Clemens 的聲明。K 和 ¬K 都是極限融貫的。沒有任何先驗反思可以表明 Twain 是 Clemens，也沒有任何先驗反思可以表明他不是。Twain 是 Clemens 的事實無法先驗地證明。必須去看。而既然他們是同一人，他們就不能不是如此。K 不僅為真，而且真正必然為真。¬K 是真正不可能的。但它是極限融貫的。

Strugeon 打算先撇開不尋常的聲明：以索引性（indexicality）或規定性（stipulation）所掌握的聲明。

只考慮尋常聲明。假設，一個聲明只要沒有證明其相反，便是可能的。產生了一個先驗劃分：

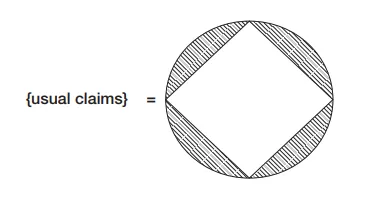
陰影區域包含了極限不融貫性，內部菱形包含極限融貫性。

Kripke 的論證顯示後者的劃分嵌入在非陰影區域內。圖示如下：

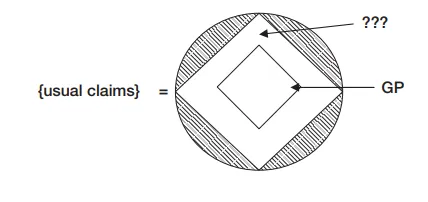
內部菱形將真正可能性和不可能性分開。外部菱形將極限融貫性和不融貫性分開。問號的空間稱作「Kripke 區」。包含像 ¬K 這樣的尋常聲明：它們是極限融貫的，卻是真正不可能的。

Kripke 的策略依賴這樣的聲明：

• 關於現實事實的聲明；
• 這些聲明本身及其否定是極限融貫的；
• 這些聲明本身及其否定涉及的問題被先驗地認為是非偶然的。

考慮這樣的聲明，我們定義：當 $\phi$ 在根據 Kripke 真理時極限融貫時，$\phi$ 是 Kripke 融貫的，表達為：

• $\text{kc}(\phi) = \text{lim}(\phi/K)$

其中 K 是為真的 Kripke 聲明集。

對 Kripke 的最保守反應：承認 (l) 有反例，但認為 Kripke 融貫性不可錯地標記了真正的可能性。

將 (l) 替換為：

• (k) $\text{kc}(\phi) \rightarrow \Diamond \phi$

這觀點承認極限融貫性的空間超過了真正可能性的空間，但要從前者縮小到後者，只需要排除為假的 Kripke 聲明。

但問題是，有 Kripke 融貫但不真正可能的聲明存在。考慮 $L$：在真正可能性空間中的最大細粒點是特定類型的分體論總和（Lewis 的世界觀）。

L 和 ¬L 都是表面融貫的，它們也是極限融貫的，我們無法先驗地排除其中一個。有辦法有關於現實事實的真理可以排除它們的融貫性嗎？

Strugeon 認為不行，它們是 Kripke 融貫的：

• (8) $\text{kc}(L)$
• (9) $\text{kc}(\neg L)$

加入 Kripke 真理，L 和 ¬L 都保持融貫。

但 (8)、(9) 和 (k) 共同會得出：

• (10) $\Diamond L$
• (11) $\Diamond \neg L$。

這是真正不可能的：

• (12) $L \land \Diamond \neg L$。

因此：

• (13) $\Box (L \rightarrow \neg \Diamond \neg L)$。

這和 (10)（在 S5 下。或是可以關注 L 是一個同一性聲明，那就不需要使用 S5）得出

• (14) $\Box L$，

這與 (11) 衝突。

這也是真正不可能的，會有一樣的問題：

• (15) $\neg L \land \Diamond L$。

結論是，無論 L 或 ¬L 最終為真，它們都是必然的，因此 (10) 和 (11) 不能同時為真，所以至少有一個 Kripke 融貫性是真正不可能的。因此 (k) 是失敗的。

K 式對 (l) 的反例和 L 式對 (k) 的反例，共享 Kripke 在討論這些問題時強調的兩個特徵：

• (κ1) 這些聲明本身及其否定是極限融貫的；
• (κ2) 這些聲明本身及其否定涉及的問題被先驗地認為是非偶然的。

當一個聲明滿足這些原則時，它不能被先驗地排除，也不能被先驗地納入，但該聲明及其否定涉及的主題可以先驗地看作是非偶然的。

我們可以純粹先驗地看到，先驗反思必定對某些地方的不可能性不敏感。

這意味著先驗融貫性和真正可能性之間將會有進一步的系統性不融貫。

例如，設 R 是任何滿足 (κ1) 和 (κ2) 的聲明。R 和其否定都不能被先驗地排除，但先驗地 R 要麼是必然的，要麼是不可能的。

接下來考慮任何先驗獨立於 R 及其否定的偶然聲明 C。如果 R 是必然的，(C & ¬R) 是極限融貫的卻是不可能的。如果 R 是不可能的，(C & R) 是極限融貫的卻是不可能的。

一般來說：當 R 是滿足 (κ1) 和 (κ2) 的聲明時，會有一系列其他聲明具有以下兩個特徵：

• (κ1) 這些聲明本身及其否定是極限融貫的；
• (κ3) 兩聲明中至少其一，先驗地，根據滿足 (κ1) 和 (κ2) 的某些聲明的真值是非偶然的。

假設 R 是任何滿足 (κ1) 和 (κ2) 的聲明，比如「Hesperus 是 Phosphorus」。

接下來，考慮這個關於位置的聲明：

• P = Hesperus 在一個地方而 Phosphorus 在另一個地方。

P 及其否定都是極限融貫的：僅靠先驗反思無法排除它們，即使是理想的先驗反思。然而，先驗地，如果 R 為真，那麼 P 必定為假。換句話說，先驗地，如果 Hesperus 是 Phosphorus，那麼 Hesperus 在一個地方而 Phosphorus 在另一個地方是不可能的。這是先驗的，因此 P 滿足 (κ3)。

更一般地，對於任何特徵 F，由於 Leibniz 法則的先驗性，先驗地，如果 R 為真，那麼不可能 Hesperus 有 F 而 Phosphorus 沒有 F。

說 $\phi$ 是先驗開放的——或簡稱開放的——意思是：

• (κ1) $\phi$ 及 $\neg \phi$ 都是極限融貫的；
• ¬(κ3) 兩聲明中至少其一，非先驗地，根據滿足 (κ1) 和 (κ2) 的某些聲明的真值是非偶然的。

將 (k) 替換為：

• (o) $\text{o}(\phi) \rightarrow \Diamond \phi$

$o(\phi)$ 表示 $\phi$ 是開放的。

(o) 是成熟的先驗不可錯論，透過開放性不可錯地標記真正的可能性。

Strugeon 指出：

1. (o) 沒有純粹的哲學反例。因為沒有聲明可以又是開放的又是先驗不可能的，根據開放性的的第二個條件。
2. Kripke 風格的論證無法反駁 (o)，因為該論證需要依賴違反 (k3) 的聲明。

$\phi$ 是開放的，僅當它的否定也是開放的，這顯示了 (o) 的範圍過窄的問題。(o) 因此只有在開放性標記偶然性時才沒有反例。(o) 只有在這個模式也是無問題時才沒有問題：

• (o)$^*\ \text{o}(\phi) \rightarrow \phi \text{ 是偶然的}$

問題在於，有些由先驗反思標記的非偶然可能性：例如，所有事物都是自身同一的。而 (o) 完全忽略了這個。

因此我們需要為先驗必然性設計一個條件。

我們說 $\phi$ 是先驗強制（apriori forced）的——或簡稱強制的——符合以下三個條件：

1. $\phi$ 是極限融貫的，
2. $\neg \phi$ 不是極限融貫的，
3. 先驗地，這些聲明涉及的問題是非偶然的。

以 $\text{f}(\phi)$ 來表達。

$\phi$ 是先驗適當的（apriori apt）——或簡稱適當的——當 $\phi$ 是開放的或強制的，以 $\text{apt}(\phi)$ 來表達這一點，將 (o) 替換為：

• (a) $\text{apt}(\phi) \rightarrow \Diamond \phi$

這是高度成熟的先驗不可錯論。在這觀點下，適當性不可錯地標記了真正可能性，而該標記由兩條件構成。一方面，它包含了先驗必然性的狀況。另一方面它不會有先驗反例，也不會有 Kripke 式的反例能攻擊它。

基於知識論的不可錯論

1. 魔法反對

Strugeon 指出，我們有一種會混淆知識論和形上學的傾向，他稱之為「知識論與形上學混淆傾向」（ep-&-met tendency）。他認為，這可以解釋我們為何會模糊先驗容慣性、可設想性與真正可能性。

他認為這是一種誘惑，真正可能性應該要獨立於心靈與語言，作為一個非知識論的領域。因此理想化的先驗反思這樣的純粹知識論程序，應該只能是可錯的指引。知識論和形上學應該停留在這樣的契合上。

以一般的知識類比，理想的知識程序、獲得信念的過程可以是不可錯的。這作為知識會需要世界的參與，無法由人單獨完成。

而在模態的情況下，理想化的知識程序卻不涉及真正模態的參與。當 $\phi$ 是適當的，並不構成 $\phi$ 的真正可能性或是其任何成分。適當性來自知識論極限中的內在融貫性，但並不涉及模態。因此，從它到模態間的聯繫應該要是可錯的。

Strugeon 將這種反對方式稱之為「魔法反對」：如果這裡是不可錯的，由於模態事實無涉於信念的形成，這裡只能是魔法般地不可錯的。

因此，要麼真正模態的知識論是特別的，要麼不可錯論是錯的。Strugeon 出於反對理論複雜化的理由，反對這是一個例外。

2. Kripke 直覺和額外魔法反對

知識論策略通過排除 (κ3) 的先驗條件來避免先驗警告，然後聲稱結果是對真正可能性的不可錯指引。這預設了極限反思只有在落入 (κ3) 的範疇時才會在模態上出錯，這是額外的魔法：

• (X) 除非在承認聲明及其否定為融貫的同時，也承認它們存在非偶然性的危險，否則極限情況的先驗反思不可錯地描繪了真正可能性。

Strugeon 類比了一個例子：假設你有一副可錯的眼鏡。有時它們提供你環境的真實經驗，有時提供錯誤的經驗；但每當它們提供錯誤經驗時，它們也會在你的視野底部產生警告：「注意！」，它說，「這次經驗很可能是錯誤的」。假設這副眼鏡被形上學保證在沒有這種擔憂產生的情況下提供真實經驗。他表示，需要對這副眼鏡的解釋，說明它為何能夠完美運作。

但我們對這裡的極端可靠性，關於這個精細調整如何在極限融貫性和真正可能性之間實現一無所知。他將此稱為額外魔法反對。

基於語義的觀點

二維語義常被用來調和模態不可錯論和 Kripke 的直覺。

像是 $X \text{ 是 } Y$ 的聲明，有至少四種解讀，1 表示捕捉了純粹先驗意義的讀法，2 則是非先驗意義的讀法：

• (i) $X_1 \text{ 是 } Y_1$
• (ii) $X_1 \text{ 是 } Y_2$
• (iii) $X_2 \text{ 是 } Y_1$
• (iv) $X_2 \text{ 是 } Y_2$

語義的不可錯論，表明先驗反思是對真正可能性的不可錯指引：

• 如果一個聲明在所有成分概念都以純粹的先驗方式解讀時是先驗融貫的，則該聲明是真正可能的。

語義不可錯論的問題

語義觀點認為這模式沒有反例，只要 $\phi$ 概念是在先驗語義維度上解讀：

• (l) $\text{lim}(\phi) \rightarrow \Diamond \phi$

Strugeon 認為這純然是魔法。如上所述的語義觀點只是借助了一個語義維度，沿其進行的極限反思就能不可錯地標記真正可能性。

他表示，語義不可錯論者幾乎沒提供積極的論證。舉例來說，David Chalmers 幾乎完全是在反對那些反對語義不可錯論的論證。他唯一的積極論證依賴於：

我們應該將我們的模態概念的根源定位於理性領域…當我們觀察模態的用途時，令人驚訝的是，許多都與理性和心理密切相關：分析思想的內容和語言的語義、解釋反事實思維、分析理性推理。可以論證，為了使可能性和必然性的概念在這些領域的分析中真正有用，它必須是一個理性模態概念，與融貫性、理性推理或可設想性本質上相關。

Strugeon 指出，這些考慮便沒有顧及到要將知識論和形上學區別開來。

額外魔法反對

Strugeon 指出，除了認為精細化的先驗條件構成不可錯的條件是魔法，認為極限反思在必然時能警告其自身的可錯性也是額外的魔法。

語義方法利用跨維度的語義分歧來先驗地解釋 Kripke 的直覺，預設了理想的推理者可以先驗地檢測出模態錯誤的危險。問題在於，我們不明白這個檢測過程是如何運作的，不明白精確的可靠性、這種精確的微調如何在極限融貫性和真正可能性之間實現。

道德追尋

因此，假設模態不可錯論是錯的。任何形式的

• ($\Box$) $\neg \text{limit-reject}(\phi) \rightarrow \Diamond \phi$

都是可錯的。那不可錯論的崩潰給我們怎樣的道德教訓？

考慮這樣的思路：

(!) 極限融貫性是某種真正可能性的指導。是什麼樣的指導？不可錯論說它是不可錯的指導，但言過其實。極限融貫性是對真正可能性的可錯指導：當 $\phi$ 通過先驗審查時，這是認為 $\phi$ 可以真正發生的理由；但這理由是可錯的。「為何如此」是個好問題，但「是否如此」則不是。極限融貫性可錯地標記真正可能性是毫無疑問的。這事實是模態實踐的基石，沒有它就沒有實踐。

Strugeon 反省，他現在不認為這是合理的了。因為這思路是知識論與形上學的混淆傾向所引起的。

(!) 的第一句話是錯的，通過先驗審查顯然不是對真正可能性的指導，而只是對可能性的指導。基本數據是無限定的：

• (BEDROCK) 極限融貫性是某種可能性的指導。

這是一個數據：未被先驗排除是可能性的標記，我們必須在 (BEDROCK) 中找到真理。這原則的日常狀態的關鍵後果是，其模態概念是前理論的（pre-theoretic）。前理論有其需要清除的混淆，我們需要找出更精煉的概念繼承前理論的真理。

考慮 (BEDROCK) 經過知識論和形上學的雙重清理：

• (E) 極限融貫性是可設想性的指導。
• (M) 極限融貫性是真正可能性的指導。

E 是顯而易見的，而且極限融貫性是可設想性的不可錯指導也是顯而易見的。這並不能確保 (M)。

先驗主義關於真正可能性的真實性並不明確，只是因為這問題不是前理論的，無法由日常承諾和直覺所擔保。

同樣的觀點適用於先驗反思和真正必然性。考慮規則：

• ($\Box$) $\text{limit-adopt}(\phi) \rightarrow \Box \phi$。

一個命題是否被先驗地裁定是一個純粹的認識論事實，這是一個理想化的認識標誌，表明先驗推理所遵循的規範強制我們接受該聲明。但一個命題是否真正必然是純粹的形而上學事實，這是一個非認識論的標誌，表明所有真正的模態實在都被該聲明正確描述。但兩標記是獨立的。

這是否有認知不融貫的問題？概念上為真的義務看起來是必然的，如果是這樣，那真正必然性的可錯論便不能成立。

Strugeon 指出，這起源一個混亂的模式：

• (BEDROCK$^*$) $\text{如果極限反思採用} \phi \text{，那麼必須是} \phi$。

這同樣涉及知識論、形上學的混淆。這個前理論的數據可以有兩種解讀：

• (E$^*$) $\text{如果極限反思採用} \phi \text{，那麼必須採用} \phi$。
• (M$^*$) $\text{如果極限反思採用} \phi \text{，那麼它是真正必然的} \phi$。

(E$^*$) 是顯而易見的，先驗確定和極限義務是同樣的「必須」。但這並不能確保 (M$^*$)。這無法由前理論的領域所擔保。

關鍵

首先我們可以注意到 ($\Box$) 等價於 ($\Diamond$) 的逆聲明。

因此兩個原則共同提供了：

• (v) $\neg \text{limit-reject}(\phi) \equiv \Diamond \phi$。

我們用 $\Diamond? (\phi)$ 來表示 $\phi$ 是概念上可能的（也標記了這個概念的模糊性）。我們有以下假設：

• (vi) $\neg \text{limit-reject}(\phi) \equiv \Diamond? \phi$。

理想情況下：一個聲明若不是概念上可能的，便會被先驗排除。或者說：一個聲明只有在它是概念上不可能的，才應該被先驗排除。這和 (v) 得出雙條件句：

• (≡) $\Diamond? \phi \equiv \Diamond \phi$。

關於真正模態的先驗論取決於兩個模式：$(\Diamond)$ 和 $(\Box)$。它們直接導致 (≡)。

這樣想。將所有尋常聲明放在一區域中，從其餘中標記出概念可能性，將它們的區域塗成黃色：

將所有尋常聲明放在一新區域中，從其餘部分中標記出真正可能性，將它們的區域塗成藍色：

疊起來：

圖說：

• 黃色是概念上可能但不是真正可能的，這是 $(\Diamond) \neg \text{limit-reject}(\phi) \rightarrow \Diamond \phi$ 的反例。
• 藍色是真正可能但不是概念上可能的。它們的否定是先驗強制的，但不是真正必然的，這是 $(\Box) \text{limit-adopt}(\phi) \rightarrow \Box \phi$ 的反例。
• 關於真正模態的先驗主義取決於概念和真正可能性對齊的程度，取決於它們結合成「綠色」的程度。

在這裡可以假設有不同的建構世界的圖景。一個可能性最豐富的假設，是真正可能性和概念可能性融貫的觀點。而可能性最稀缺的假設，是認為真正可能性和自然法則可能性融貫的觀點。而真相可以位於光譜之間：

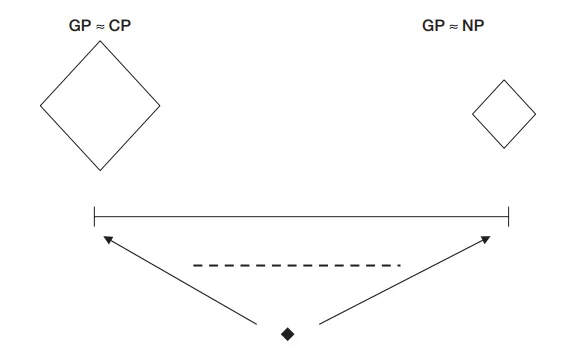
即便現在不討論總體理論，我們依然可以說：先驗反思對真正模態的指引，其實在於真正可能性有多豐富——也就是說，在於它是否與概念可能性融貫：

• 如果有非瑣碎的融貫性：極限融貫性將是對真正可能性的有用指引，而極限義務將是對真正必然性的有用指引。
• 如果沒有非瑣碎的融貫性：先驗反思將對真正模態無用。極限融貫性將不標記真正可能性，極限義務將不標記真正必然性。

有充分理由認為極限融貫性並不能不可錯地標記真正可能性。這基於我們對知識論和形上學契合的最佳理解。然而，極限融貫性很可能可錯地標記真正可能性，取決於真正和概念可能性對齊的程度。

有充分理由認為極限義務並不能不可錯地標記真正必然性，這也取決於知識論和形上學的契合。然而，極限義務很可能可錯地標記真正必然性，這也將取決於真正和概念可能性對齊的程度。

當涉及對齊本身時，我們的觀點應取決於如何最佳地系統化思維。如果假設豐富的真正可能性比不這樣做能更好地系統化總體理論，那麼我們應接受概念和真正模態之間的融貫性。這意味著極限融貫性是對真正可能性的好的但可錯的指引，而極限義務是對真正必然性的一個好的但可錯的指引。

我們無法說明融貫性是否存在。但我們可以說：關於真正模態的先驗論取決於它是否存在。

附錄：刻畫 Kripke 區域

「$\text{accept}(\phi)$」表示理想的先驗推理者會接受 $\phi$，「$\text{reject}(\phi)$」表示他會拒絕 $\phi$。

當以下兩者為真時，聲明被稱為未解決——簡寫為「$\text{un}(\phi)$」：

• $\neg \text{reject}(\phi)$，
• $\neg \text{reject}(\neg\phi)$。

在 Kripke 和 Putnam 的後驗必然性研究前，未解決足以構成真正可能性：

• (un) $\text{un}(\phi) \rightarrow \Diamond \phi$。

假設 $K$ 聲明 Mark Twain 和 Jack Kennedy 是同一個人。理想的先驗推理將支持：

• $K \lor \neg K$，
• $K \rightarrow \neg \Diamond \neg K$，
• $\neg K \rightarrow \neg\Diamond K$。

得出：

• $\neg\Diamond \neg K \lor \neg\Diamond K$。

先驗推理也支持：

• $\text{un}(K) \land \text{un}(\neg K)$。

接著可以得出：

• $[\text{un}(K) \land \neg\Diamond K] \lor [\text{un}(¬K) \land \neg\Diamond \neg K]$。

由此可以得出：

• $(\exists \phi)[\text{un}(\phi) \land \neg\Diamond \phi]$。

以上是後驗必然性的先驗存在證明。

推動上述證明的關鍵洞見是，存在聲明 $\phi$，使得：

• $\text{un}(\phi)$，
• $\text{accept}[\neg\phi\rightarrow \neg \Diamond \phi]$。

我們將 $\phi$ 稱為「KP-聲明」——簡寫為「$\text{kp}(\phi)$」。

如果一個聲明滿足下面兩件事，稱之為內在乾淨的（intrinsically clean）——寫作「$\text{int}(\phi)$」：

• $\text{un}(\phi)$，
• $\neg\text{accept}[\neg\phi\rightarrow \neg\Diamond \phi]$。

對證明的自然回應是承認 (un) 無效，但堅持這模式：

• (int) $\text{int}(\phi) \rightarrow \Diamond \phi$。

有兩個案例表示 (int) 是無效的。

案例 1. 讓 $\phi$ 成為假的 KP-聲明，然後讓 $\psi$ 成為一個與 $\phi$ 先驗無關的未解決聲明，也就是說，滿足：

• $\text{un}(\psi)$，
• $\neg\text{accept}[\phi \rightarrow \psi]$，
• $\neg\text{accept}[\psi \rightarrow \phi]$。

然後我們有：

• $\text{un}(\psi)$，
• $\neg\text{accept}[\neg(\phi\land\psi)\rightarrow\neg\Diamond(\phi \land \psi)]$。

這是 (int) 的反例，我們同時有：

• $\text{int}(\phi\land \psi)$，
• $\neg\Diamond (\phi \land \psi)$。

案例 2. 讓 $\phi$ 成為 Hesperus 有一個 Phosphorus 所缺乏的特徵的聲明：

• $\text{un}(\phi)$，
• $\neg\text{accept}(\neg\phi\rightarrow \neg\Diamond \phi)$。

但 $\phi$ 是不可能的，因此這也是 (int) 的反例。

在這兩案例中，若 KP-聲明為真，則相關的 (int) 反例是不可能的。

若下面兩件事情發生，聲明 $\phi$ 是完全乾淨的（fully clean）——寫作「$\text{clean}(\phi)$」：

• $\text{un}(\phi)$，
• $\neg(\exists\psi)\{\text{kp}(\psi)\land \text{accept}[\psi \rightarrow \neg \Diamond \phi]\}$。

完全乾淨性只是未解決性減去製造麻煩的 KP-聲明。

對上述案例的自然回應是承認 (int) 是無效的，但堅持這模式有效：

• (clean) $\text{clean}(\phi) \rightarrow \Diamond \phi$。

給定一個未解決的聲明 $\phi$，設 X 為 $\phi$ 不是真正可能的聲明。假設可以先驗地證明某些聲明是未解決但不是真正可能的。那麼先驗推理不能排除 $\phi$ 不是這樣的東西。意味著 X 本身是未解決的，因為：

• $\neg\text{reject}(X) = \neg\text{reject}(\neg\Diamond \phi)$，
• $\neg\text{reject}(\neg X) = \neg \text{reject}(\Diamond \phi)$。

但這顯然是：

• $\text{accept}(X \rightarrow \neg\Diamond \phi)$。

因為 X 是 $\phi$ 不是真正可能的聲明。如果 X 是一個 KP-聲明，意味著 $\phi$ 不是完全乾淨的；因為 X 會是未解決的聲明，滿足 $\phi$ 的乾淨性定義中的量詞。如果以下內容也是正確的，X 就是一個 KP-聲明：

• $\text{accept}(\neg X \rightarrow \neg\Diamond X)$。

這等價於：

• $\text{accept}(\Diamond \phi \rightarrow \neg\Diamond \neg\Diamond \phi)$。

又等價於：

• $\text{accept}(\Diamond \phi \rightarrow \Box \Diamond \phi)$。

這是 S5 的特徵式。因此，如果先驗地認為 S5 是真正可能性的正確邏輯，則 X 會是 KP-聲明，$\phi$ 會變得不完全乾淨。

因此：

如果我們的存在證明的先驗性質使得像 X 這樣的聲明未解決，並且先驗地理解真正可能性的邏輯是 S5，那麼沒有未解決的聲明是完全乾淨的。

C. S. Jenkins 回應 Scott Strugeon

1

Jenkins 指出，不可錯的先驗論者相信在先驗融貫和可能性間存在一個有知識論意義的聯繫，並且這並不能很好地被實質條件句所捕捉，因為實質條件句可能無法在兩者間建立這個聯繫。

乍看之下，Strugeon 的不可錯誤論的實質雙條件句版本似乎避免了這種擔憂。這個條件句是：

• (≡) $\Diamond? \phi \equiv \Diamond \phi$。

概念上可能與真正可能的等價性。在這情況下，如果仍有真正可能的東西，但沒有東西在概念上可能，那雙條件便不會成立。這問題也影響了使用物質雙條件句來嘗試捕捉先驗反思作為模態事實的良好知識論指導的論點。

考慮以下類比：

• Gullible（壽命無限的人）跟隨模態大師（另一個壽命無限的人）學習。Gullible 相信大師在無限的時間內會說出所有且僅有的可能的事。Gullible 盲目地接受大師說的一切即為可能性，儘管 Gullible 沒有充分理由相信大師。但事實上，大師確實說出了所有且僅有的可能事情。

考慮：

• (g) $\text{guru}(\phi) \equiv \Diamond\phi$。

在所設想情況下這是正確的。但斷言其真實性，並不能證明盲目相信大師是模態事實的良好知識論指導（即獲得這些事實的知識的一種方式）。

Jenkins 表明，使用實質雙條件句來捕捉知識論論題，如 Strugeon 所做的，是在假設非常粗略的可靠論形式。Strugeon 在最後的段落中強調概念可能性和真正可能性之間的對齊，是出於同樣的問題。

(k) 主張「 Kripke 融貫性」在實質上意味著可能性。Kripke 融貫性是指在「 Kripke 真理」的光照下的極限融貫性。Kripke 真理是非模態的真聲明，它及其否定都是極限融貫的，而且是先驗義務的（它所提出的問題是非偶然的）。

Strugeon 接著稱，存在 Kripke 融貫的聲明並非真正可能性，從而是 (k) 的反例。

他的例子是 $L$：「Lewis 世界能使真正模態的聲明成為真聲明」。

他說，$L$ 和 $¬L$ 中至少有一個不是真正可能的，但它們都是 Kripke 融貫的。

Strugeon 認為它們是 Kripke 聲明，因為它們滿足他給出的成為 Kripke 聲明的條件：

• 它們是非模態的，
• 它們都是極限融貫的，
• 無論 $L$ 和 $¬L$ 哪個為真，它都是必然的。

Strugeon 的關於「先驗融貫性和真正可能性間的系統性對不齊」似乎是進一步的 (k) 反例，並進一步動機推動轉向 (o)。但 Strugeon 沒有證明這些是 (k) 的反例。

以 Strugeon 的例子 $(C \& R)$ 和 $(C \& ¬R)$ 為例，其中 $R$ 是：它及其否定都是極限融貫的，但先驗義務是其提出的問題是非偶然的，而 $C$ 是獨立於 $R$ 及其否定的偶然聲明。

假設 $R$ 和 $¬R$ 是 Kripke 聲明。那麼其中一個是 Kripke 真理。如果 $¬R$ 是 Kripke 真理，那麼 $(C\&¬R)$ 即便是極限融貫的，它也不是 Kripke 融貫的。因為它被一個 Kripke 真理 $R$ 所排除。同樣，如果 $¬R$ 是 Kripke 真理，那麼 $(C\&R)$ 即使它是極限融貫的，它也不是 Kripke 融貫的。

要找到 (k) 的反例，Strugeon 需要證明存在符合 $R$ 條件的聲明，而這些聲明不是 Kripke 聲明。

$R$ 的條件是成為 Kripke 真理的三個條件中的兩個，唯一的選擇是證明某些聲明符合 $R$ 的條件但不符合 Kripke 聲明的最終條件，即它們是模態的。

一種符合 $R$ 條件的明顯模態聲明是同一性聲明的模態版本，例如：Mark Twain 即是 Sam Clemens。我們就稱作 $R$。然後以 $P$ 表示無模態的「Mark Twain 即是 Sam Clemens」聲明。

但 $R$ 不會是 Strugeon 設想的 (k) 的反例。即使 $(C\&R)$ 和 $(C\&¬R)$ 都是極限融貫的，其中一個不是 Kripke 融貫的。因為 $P$ 和 $¬P$ 之一是 Kripke 真理：

• 如果 $P$ 是 Kripke 真理，那麼 $¬R$ 是真正不可能的，$(C\&¬R)$ 也是。但這樣的話 $¬R$ 與 $P$（一個 Kripke 真理）不融貫，因此 $¬R$ 不是 Kripke 融貫的。所以 $(C\&¬R)$ 也不是 Kripke 融貫的。
• 如果 $¬P$ 是 Kripke 真理，那麼 $R$ 是真正不可能的，$(C\&R)$ 也是。但這樣的話 $R$ 與 $¬P$（一個 Kripke 真理）不融貫，因此 $R$ 不是 Kripke 融貫的。所以 $(C\&R)$ 也不是 Kripke 融貫的。

所以我們無法這樣證明 $(C\&R)$ 和 $(C\&¬R)$ 之一是 Kripke 融貫且是真正不可能的。

「$L$」是指 Lewisian 世界使真正模態的聲明成為真聲明。Strugeon 認為，不可能是

• (12) $L \& \Diamond ¬L$。

他的理由是，第一個連接項蘊含了，第二個要為真，必須有個 Lewisian 世界，而在該世界中，該世界不存在。Jenkins 認為，這裡其實只蘊含有個 Lewisian 世界，而在該世界中，該世界不是任何模態聲明的使真者。所以要令 $¬L$ 為真的方式的一種方式是，Lewisian 世界使一些但非所有的真正模態聲明成為真聲明。現在，在該世界，所有模態聲明都是由 Lewisian 世界成為真聲明。因此，$L$ 為真，但有一個世界 $w$，有一些但非所有模態聲明都是由 Lewisian 世界成為真聲明的，並且 $w$ 自身也是一些模態聲明的使真者。

Strugeon 引用了 Lewis，聲稱 Lewis 是為了將概念可能性與真正可能性對齊。

Jenkins 反對這樣的解讀，Lewis 只是在論證相信可能世界本體論的成本是由信念的理論收益所證成的。「概念」模態沒有出現在 Lewis 的論述裡，Lewis 說的是「邏輯」。而 Strugeon 認為，Lewis 所說的邏輯模態即是 Strugeon 所說的「真正」模態。

Strugeon 在結論中主張：「先驗反思是對真正模態的指引，在於真正可能性是否豐富——也就是說，在於它是否與概念可能性融貫。」

看來 Strugeon 假設真正模態不能太豐富而無法與概念可能性很好地融貫。但有些例子可以表明真正可能性其實超出了概念可能性。例如，非歐幾何作為物理空間的理論，以及量子力學中的某些結果，有理由被認為是概念上不融貫的，但不僅是真正可能的，還是現實上為真的。

2

Jenkins 首先談論了實在論的知識論。所謂的「實在論地解釋的主題」，指的是我們傾向於對該主題持心靈獨立的實在論的看法。對於如何知道該主題的解釋，似乎符合三步原則：

1. 某種世界輸入進入我們的心理過程。
2. 進行某種心理處理。
3. 形成一個信念。

對此 Jenkins 表示，Strugeon 設想的使聲明為真的方法，似乎不符合實在論知識論的模式。第二和第三步還好（或者說，儘管它們還沒有完全解釋清楚，但至少看起來不是顯然有問題的）：在這種情況下的心理處理是某種內省調查你能設想什麼，在這過程結束後，我們形成了一個信念。但第一步呢？

Strugeon 的「魔法」和「額外魔法」擔憂都是對理想化的可設想性的不可錯的擔憂，對於那些接受以下實質條件句的人的擔憂：

• IC： (模態信念 $B$ 是通過理想化的可設想性方法獲得的) $⊃$ (模態信念 $B$ 為真)。

但 Strugeon 對對應的理想化視覺的主張並不感到困擾，即：

• IV： (信念 $B$ 是通過理想化的視覺獲得的) $⊃$ (信念 $B$ 為真)。

問題在於，與理想化的可設想性相關的「理想化」與輸入步無關，這樣真理保證如何能有空間？

Jenkins 表示，不可錯並不是生成 Strugeon 的擔憂所需的。如果我們能將滿意的輸入步驟包括在我們的可設想性方法中，然後將該步驟的理想化包括在可設想性方法的理想化中，那 Strugeon 的擔憂將被解決。

Jenkins 接著表示，現在這問題是一個非常普遍的問題的實例，即解釋我們如何擁有先驗知識——這似乎不需要來自心靈獨立世界的輸入——屬於某些心靈獨立領域的事實。這也是一個非常古老的問題，已經有許多現存的答案，例如：

• 理性主義者可能會聲稱理性直覺以某種方式為可設想性方法提供輸入（如 Bealer 2000，BonJour 1998）。
• 一些人認為缺乏任何合理的輸入步是拒絕關於模態真理的心靈獨立實在論的理由；他們可能採用某種 Ayer 或 Carnap 的反實在論（見例如 Ayer 1936，Carnap 1950a）。
• 一些人認為，可設想性方法不能是我們獲得（心靈獨立的）模態真理的方法，因為它不涉及輸入步。相反，他們論證我們必須使用普通經驗方法（見例如 Mill 1891，Quine 1951）。
• Jenkins 則主張，可設想性方法涉及經驗輸入步。我認為經驗輸入使我們的概念成為理解世界的良好指引，從而我們可以通過設想各種情景的實踐，從這些概念中恢復關於世界的信息（見 Jenkins 2008）。